The Markov model in pharmacoeconomics is used to simulate clinical and economic effects of treatments, compare healthcare programs and aid decision making.
What is the Markov model?
The Markov model is a mathematical model involving a particular series of mutually exclusive and exhaustive health states with transition probabilities from one state to another. It also includes the likelihood of remaining in the current state. Usually, the time to stay in any state is the same, and the transition probabilities remain constant. The Markov model in pharmacoeconomics is used to estimate the cost-effectiveness of treatment programmes (prevention, hospital care, etc). It also has wide application in applied fields: economics, logistics, marketing.
The Markov model in health economics generalizes a patient flow process. The principles are:
- Disease can be characterized by mutually exclusive states covering the full spectrum of disease manifestations.
- Probabilities of transition from one state to another depend only on the current state but do not depend on the previous ones.
- Probabilities of transition from one state to another are independent of time (homogeneity).
The New York Heart Association Failure Model (NYHA) and the type 2 diabetes prevention program are examples of its use. Markov model cost-effectiveness is proved in practice.
Construction of a Markov model
The construction of a model begins with a graphical representation.

Graphical representation: transitions from state 1
The basic relationship for state 1 is: p(11) + p(12) + p(13) + p(14) + p(15) = 1
Once in state 2, the patient can go back to 1, stay in 2, go to 3, 4, 5, or, if in the terminal state, remain in it.
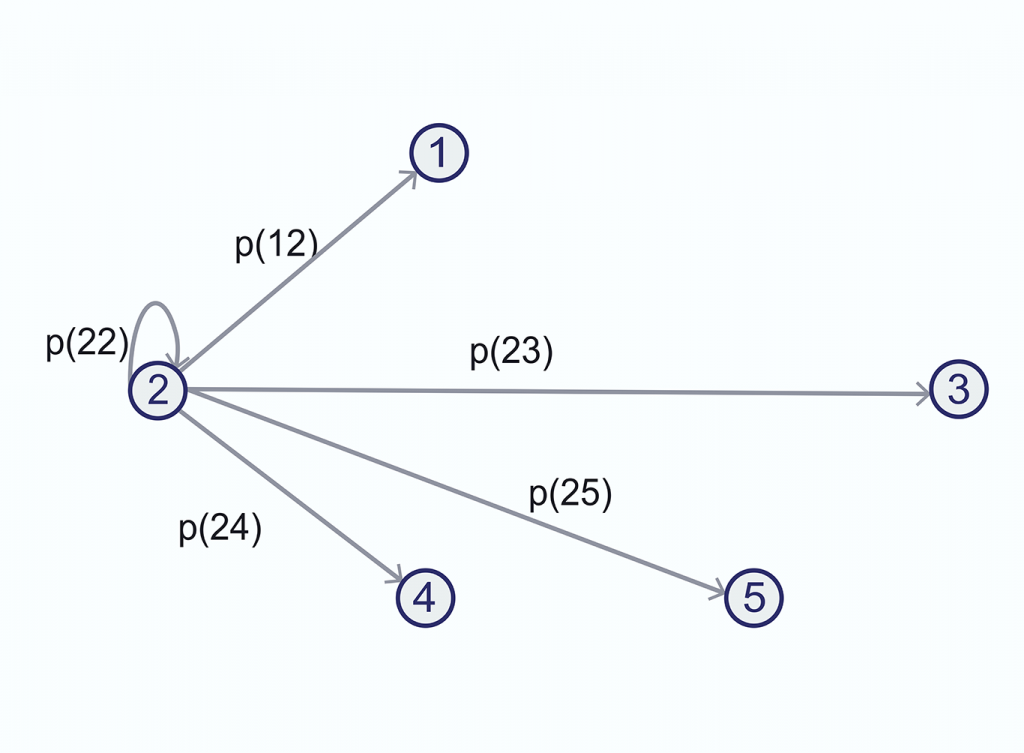
Transitions from state 2: drawing back arrows
If we do this, we obtain the following:
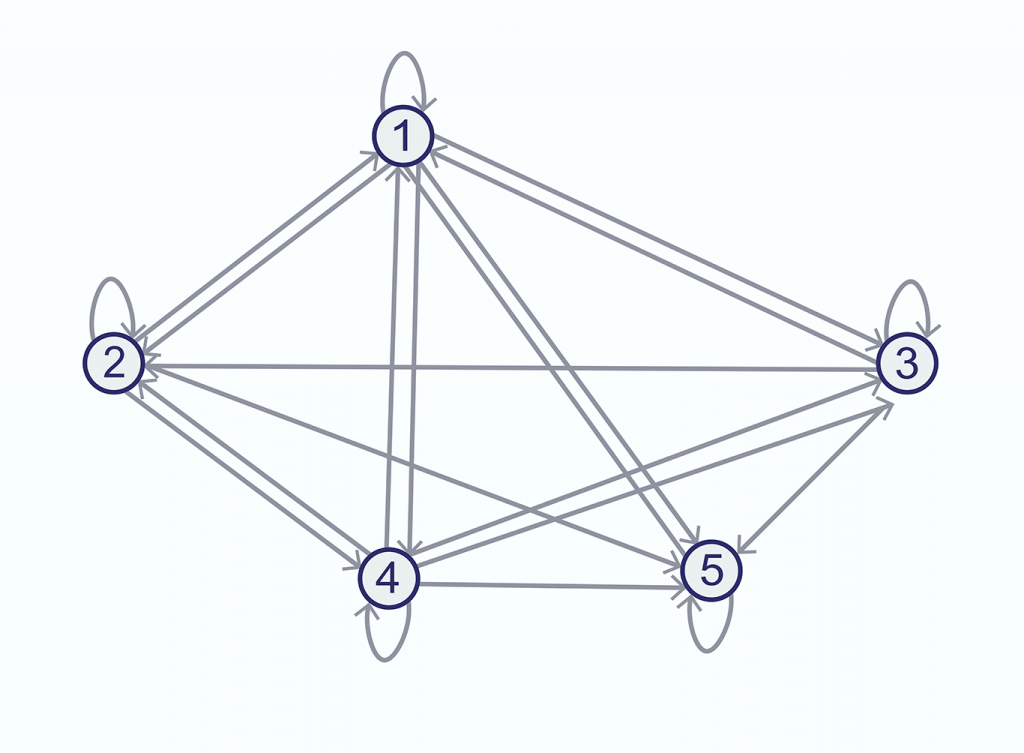
We end up with a graphical representation of the model.
Technically, the model is reduced to successive multiplication of the probability matrices and estimating the simulated number of patients at each stage. It assumes that patients are observed first in one time interval and then in another time interval (e.g., first year and then the second year, etc.). The shorter the cycle length, the more accurate analysis you can perform. Patient trajectory: if the patient enters a new condition, they move on to the next one regardless of the prehistory.
When a person develops a disease, it results in associated costs and changes in quality of life. All these events are described using Markov states.
What is Markov state?
A Markov state is a particular state of health. Each state is constant over a fixed time interval (cycle length). It is assumed that all information associated with a specific subject is consistent during each cycle.
At the end of the cycle, a further hypothetical condition of the person is evaluated. For example, what would happen to him if the patient was in complete health? Would he develop a disease or not?
The set of all probabilities of transition from one state to another is called the transition probabilities matrix. It is usually represented in the form of a table, where the rows contain the initial states and the columns include the conditions that the patient may fall into by the end of the cycle. So, the Markov model is vital for health economics.
How is the Markov model used in healthcare?
Markov models and cost effectiveness analyses are essential for healthcare decision-making. They are used when there is a synchronization (connection in time) of events, and important events can happen repeatedly. Analysis is recommended when:
- The event’s timing may affect the outcome (e.g., early cancer detection versus late detection leads to better treatment outcomes).
- The timing of the event is not precisely defined.
- Clinical decisions affect outcomes whose occurrence is related to different stages of the patient’s life.
The application of the model is appropriate when the disease can be divided into a series of sequential phases (e.g., baseline – complete health, terminal – patient death, intermediate – stages of the disease, stages of diagnosis or treatment). It assumes that the patient is always in one of the possible conditions. The transition from one condition to another is always possible, and the probability of such a transition is known. All events represent a transition from one state to another. So, the Markov model is an essential instrument in health economics and healthcare.
Thus, for example, people who are not diagnosed with disease are represented as healthy. When they detect their illness, they find themselves in the corresponding state (for example – in the initial or terminal stages of the disease). Some of the patients had an initial earlier stage, with a transition to later stages. Some patients, on the contrary, evolved from later stages to earlier ones (e.g., due to active treatment).
How does the Markov model work?
The time interval of the study is divided into equal time intervals (Markov cycles). The duration of the cycles is chosen so that each of them represents an interval of time that has a specific value in the course of treatment. For example, effectiveness evaluates only after six months of treatment with ACE inhibitors for heart failure. 6 months are spent on dose titration and slow reverse development of pathological processes in the vascular wall – vascular remodeling. Typically, in clinical and economic analysis, the cycle is taken as one year since most multicenter studies of drug efficacy evaluate the effectiveness for this period. But the model can also consider shorter cycles – 6 months, a month, sometimes a week, and they can be more succinct when studying acute diseases emergencies.
It implies that a patient can make only one transition from one condition to another during each cycle. The probability of change can remain constant or vary throughout the observation period. No distinction is made between different patients in each state. This constraint (Markov assumption) shows the development of the process after each cycle. The model retains no memory of any events in the earlier cycles.
Markov assumption
The Markov assumption often contradicts reality. It is recommended to provide several conditions with different transition probabilities. It is possible to include “temporary conditions” in which the patient can stay for some short time (shorter than the cycle), after which the patient will undoubtedly go to other conditions. According to modeling conditions, they cannot stay in the “temporary” condition. For example, if there is a risk of stroke or heart attack, this condition can be included as “temporary”. The patient cannot remain in a given acute condition for a long time. After a certain period, he is bound to move to another one (at least, he will recover or die).
Markov process
Markov model cost-effectiveness is undoubted. The process is usually represented as a state transition diagram. The probability of transition from one state to another during a single cycle is called transition probability. Some transitions are only possible in a similar sequence going through a tunnel. Therefore, they are called tunnel states, and transitions are called tunnel transitions. Tunnel states and transitions can last for more than one cycle.
For a process to stop, there must be at least one condition of health that the patient cannot get out of. The most commonly used absorbing condition in medical calculations is a patient’s death. It can also be the development of a stroke or heart attack, amputation of a limb, development of kidney failure, or disability.
A process is defined by the probability distribution between the starting conditions and the degree of transition probability allowed for particular patients (i.e., the percentage of patients of each stage of disease who recover, suffer complications, or die). So, the Markov model for cost-effectiveness analysis is the proper solution for disease modeling.
A standard method of representing is a Markov cycle tree. The Cost-effectiveness of the Markov model is proven in practice.